María del Socorro Rivera Casales | 15/04/2018

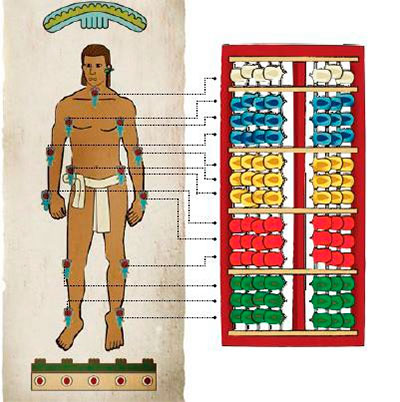
En el marco teórico se hablara del desarrollo del número natural de acuerdo a los autores: Baroody, A.J. (1988), Kamii, C. (1984), Lovell, K.(1999) y de Piaget, J. e Inhelder, B.(1978a),se enunciara el uso del  ábaco nepohualtzintzin como recurso primordial didáctico de cálculos mentales con un razonamiento-lógico en el aprendizaje de la aritmética. El método es de corte cualitativo, donde los instrumentos a utilizar en la toma de datos serán: taller a docentes y alumnos del uso del ábaco nepohualtzintzin,  cuestionarios exploratorios, entrevistas semiestructuradas, sesiones de enseñanza, diseño, aplicación y forma de análisis de cada instrumento.

1.  Introducción

1.1     Antecedentes del problema.

Una problemática en la enseñanza de las matemáticas , es una mala enseñanza de los cálculos aritméticos, por falta de comprensión y esto da como resultado un alto índice de errores en cálculos de suma y resta , otro problema es la falta de interés de los alumnos y la falta de apoyo de los papas en casa, esta problemática crea un rezago en la enseñanza de las matemáticas en cálculos de operaciones aritméticas, los docentes de niveles posteriores siempre tienen una queja de una falta de dominio de conceptos básicos.

El presente proyecto de investigación aborda la implementación del ábaco nepohualtzintzin como material didáctico para el cálculo de operaciones de suma y resta con números naturales en educación básica, de una manera más rápida y con un razonamiento lógico-matemático   en niños de 12 a 13, cursan el primer grado  de  iniciación  universitaria,  para  dar  una  solución  a  la  problemática planteada anteriormente.

El método es de corte cualitativo, donde los instrumentos a utilizar en la toma de datos serán: taller a los docentes y alumnos sobre el uso de ábaco nepohualtzintzin, cuestionarios exploratorios, entrevistas semiestructuradas, sesiones de enseñanza, diseño, aplicación y forma de análisis de cada instrumento.

Se continuara el análisis de cada instrumento, con la toma inicial de datos, entrevista inicial con los niños, desarrollo mediante un taller para el uso del ábaco nepohualtzintzin al docente frente grupo, entrevista final con los niños.

1.2      Objetivo General

Desarrollar  la  implementación  de  material  didáctica  dentro  del  aula  “Ábaco Nepohualtzintzin” para resolver cálculos de operaciones aritméticos con números naturales  en niños de 12 a 13 años de primero de iniciación, para ir reduciendo el sesgo existente.

1.3 Pregunta de Investigación

¿Cuáles son los elementos, teóricos, metodológicos y herramientas necesarias para elaborar una propuesta de material didáctico, basado en   el ábaco nepohualtzintzin, para reducir el sesgo de  cálculos aritméticos?

¿Cuál es el sesgo existente en los alumnos de ingreso a iniciación universitaria de cálculos aritméticos?

1.4 Justificación del problema de investigación

Esta investigación pretende, implementar   el “Ábaco Nepohualtzintzin” como un  material  didáctica,  utilizándose  en  los  cálculos  aritméticos  de  números naturales en el aula, trabajando la investigación en iniciación universitaria, para reducir el sesgo de cálculos aritméticos.

Los niños deben saber operaciones de cálculo de suma y resta antes de poder dar respuesta a problemas  aditivos, es una base importante los cálculos para la enseñanza de las matemáticas, hacer hincapié que debe ir relacionando con resolución de problemas y con aplicaciones de la vida cotidiana. Por lo tanto, una   razón   para   considerar   el   problema   de   investigación,  es   afrontar   la construcción de un material didáctica mediante el ábaco nepohualtzintzin, sin perder la prioridad del conteo,  y también adaptarse: a la propuesta institucional y en como lo trabajan los niños, todo esto nos servirá para la aplicación de cálculos aritméticos con números naturales.

En la actualidad, se hace notorio un interés por interés por orientar la enseñanza de las matemáticas con aprender a aprender.

1.5 Marco teórico

El presente apartado se refiere al tópico principal de estudio  desarrollo del número natural. Se hace un recorrido por las aportaciones teóricas fundamentales mediante  las  cuales  sustenta  la  investigación.  No  se  trata  de  dar  cuenta exhaustiva de la literatura existente sino únicamente retomar aquéllas que den respuestas al problema de investigación.

Al discurrir acerca del concepto de número natural consideramos la contribución de Jean Piaget y otras, no piagetianas que nos permitirán tener una visión más amplia de diversos factores que incluyen en la construcción de este concepto en los alumnos.

1.6 Desarrollo de número natural

Al llegar a la escuela primaria comienza de manera formal la enseñanza- aprendizaje de los números naturales y por lo tanto, de forma implícita, del concepto de dichos números.

Para investigadores y docentes no es algo nuevo el hecho de que los niños. Al llegar a la escuela ya tienen algunos conocimientos. Por ejemplo, enunciar verbalmente parte de la secuencia numérica, tal vez incluso escribirla o dar respuesta a planteamientos como ¿cuánto es 2+2?   y/o similares. Sin embargo, tener el concepto de número natural es mucho más que eso.

La matemática en sí misma contiene un alto grado de abstracción, es decir, es una:

…Actividad intelectual que consiste en considerar un aspecto de la realidad o un fenómeno en sus estrictas dimensiones y cualidades, aislándolo de todo con la finalidad de poder conocerlo mejor.
(SEP, 2011)

Por lo tanto, el niño sólo alcanzará el concepto de número natural si llega a existir en su mente de manera independiente de las cosas, aparatos, acciones o circunstancias, porque aun cuando este concepto es más accesible que el de otros números no deja de ser abstracto. Y a pesar de ser uno de los fundamentos de la matemática sigue encerrado cierto misterio (Lovell, 1999).

1.6.1  Planteamientos de Jean Piaget

Piaget e Inhelder (1978a) buscaban establecer si en los sujetos las operaciones intelectuales existen de forma espontánea o se aprenden socialmente y si esas operaciones y sus estructuras están presentes en todos los niveles de desarrollo o si no, cuándo y cómo se constituyen. Recurrieron a una combinación de dos métodos llamados: de resolución de problemas y de formación de conceptos.

Una vez que las acciones cognitivas se organizan en totalidades estrechamente ligadas con una estructura definida y fuerte se constituyen las operaciones cognitivas de las cuales derivan las expresiones “pensamiento pre- operacional”, “operacional concreto” y “formal” y otros semejantes.

Para llegar de la acción a la operación hay tres pasos o etapas: desde el nivel sensorio-motor de acción directa sobre lo real, para llegar al nivel de las operaciones donde, al igual que en el anterior, hay trasformación de los real adicionando acciones interiorizadas y agrupadas en sistemas coherentes y reversibles. Intermedio, ocurre un progreso sobre la acción inmediata que se interioriza. Durante este proceso hay también obstáculos serios y nuevos (Piaget e Inhelder, 1978b).

De esta manera se observa cómo las operaciones del pensamiento alcanzan su forma de equilibrio cuando se constituye en sistemas de conjunto caracterizados por su composición reversible, es así como se construyen los conceptos.

Al llegar a lo anterior, uno de los criterios más claros de la aparición de las operaciones en el nivel de las estructuras concretas se hace evidente: la constitución de invariantes o ideas de conservación; éstas se abordarán en el siguiente apartado.

1.6.2 Estructuras de agrupación y constitución de número natural

A la formación de operaciones corresponde también la constitución de estructuras operacionales de conjunto que se manifiestan de forma espontánea y pueden proceder sólo de manera progresiva. Dado lo anterior, se considera agrupamiento a un sistema que mediante una operación dada puede incluir otros elementos, ser invertido el producto (de la operación) y su inversa es una operación idéntica por no agregar ni quitar nada con la segunda operación; esto último limita a la movilidad del sistema (Piaget e Inhelder, 1978a).

La composición aditiva de las clases. La seriación de las relaciones y la generalización operatoria del número se constituyen de manera sincrónica hacia los 6-7 años, se supera el nivel pre-lógico; es en este momento cuando el niño alcanza el nivel de la operación reversible y simultáneamente es capaz de incluir, seriar y enumerar. Es así como se ha complementado la construcción operatoria aplicada: las equivalencias, las diferencias o las equivalencias, las diferencias o las equivalencias y diferencias reunidas. Al desarrollar lo anterior, va teniendo lugar la función del mecanismo aditivo en sí mismo .

Número natural. Con la constitución de estructuras que permiten el desarrollo de operaciones observables en cada una de sus etapas al aparecer ciertos   criterios   como   son   las   invariantes,   las   colecciones   figúrales,   las colecciones ulteriores, la combinación de procedimientos ascendentes y descendentes, la seriación, todas ellas ocurren de manera progresiva y su construcción ulteriores, la combinación de procedimientos ascendentes y descendentes, la seriación, todas ellas ocurren de manera progresiva y su construcción conduce a la serie de los números naturales. Lo que constituye el número es la síntesis de agrupamientos (clases, inclusión) abstracción y orden serial (Piaget e Inheler, 1978a).

La teoría Piagetiana abordada hasta aquí, coadyuva para nuestro estudio con lo siguiente:

    El diseño de los instrumentos de inicio y fin de la toma de datos, es decir, el cuestionario y las entrevistas.

    El análisis de los datos obtenidos con los instrumentos mencionados en el punto anterior.

    Con lo anterior, determinar el nivel de desarrollo de número natural en los niños al inicio y fin del estudio.

Página siguiente

ARTÍCULOS RELACIONADOS

• Implementación de material didáctico: ábaco Nepohualtzintzin (Parte II)
• La influencia de España en la enseñanza de las matemáticas a México en el siglo de oro (Parte II)

OTROS TEMAS

Encuesta