Espacio Logopedico
Tema quincena | Detección | Orientación | Interdisciplinario |
Profesionales | Glosario | Patologías | Actualidad
Comprensión de ideas fundamentales de estadística y probabilidad en el bachillerato
El artículo concierne a la comprensión de ideas fundamentales de estocásticos (Heitele, 1975) de estudiantes del nivel medio superior donde se imparte Estadística y Probabilidad como materia obligatoria o como materia optativa.
1. Primera etapa: Documental.
La enseñanza se rige por lo indicado en la propuesta institucional (ENP, 1996). El análisis de cada unidad proporcionó la poca importancia que se otorga en el bachillerato a la enseñanza de la estadística y probabilidad en general (Rivera, 2012) y se otorga prioridad a otros contenidos matemáticos y a la resolución de ejercicios.
2. Segunda etapa: Indagación
Una experiencia de la enseñanza en aula.
En el aula se desarrolló la práctica de la enseñanza mediada por el texto recomendado en el programa de estudio (Infante, 1991). La Tabla 1 resume las características de las sesiones desarrolladas.
| 1.Espacio muestral | Cálculo | Espacio muestra Independencia | Espacio muestra, población, independiente, Lanzamiento | Arreglo numérico , notación de conjuntos y lengua natural escrita |
| 2.Experimentos y eventos | Cálculo | Espacio muestra Independencia | Experimento y evento | Arreglo numérico notación de conjuntos y lengua natural escrita |
| 3.Principio fundamental de conteo | Cálculo | Espacio muestra Combinatoria Independencia | Experimento, aleatorio, repetición, sin repetición | Arreglo numérico y lengua natural escrita |
| 4.Análisis combinatorio | Cálculo | Espacio muestra Combinatoria Independencia | Ordenaciones, permutaciones, combinaciones con o sin repetición | Arreglo numérico, diagrama de árbol y lengua natural escrita |
| 5.Concepto de probabilidad | Cálculo y funcional | Medida de probabilidad, Espacio muestra, Regla del producto e independencia, Combinatoria, Equiprobabilidad y simetría, Variable aleatoria | Probabilidad, espacio muestra, casos totales, difícil | Arreglo numérico y lengua natural escrita |
Durante las tres primeras sesiones en este escenario la práctica docente ignoró la situación original planteada en cada tema y se centró en desarrollar los temas respectivos como anteriormente se hacía.
Análisis de los cuestionarios.
El objetivo general del instrumento fue recopilar datos de los conocimientos de estadística y probabilidad adquiridos aplicando dos cuestionarios, antes y después de la enseñanza en aula.
Antes de la enseñanza
El cuestionario presenta diez preguntas abiertas, en secuencia de acuerdo a la propuesta institucional de nivel básico, y en dos versiones “A” y “B” a un grupo de 43 estudiantes. Sólo 16 de los 43 estudiantes (37.21%) proporcionaron respuestas correctas a los reactivos, las preguntas; 2, 6 y 8 (modalidad A) resultaron los más difíciles. 24 estudiantes (55.81%) proporcionaron respuestas incorrectas correspondientes al procesamiento no consciente. 16 estudiantes (37.21%) dieron respuestas correctas de la etapa de la conciencia y sólo tres estudiantes (6.98%) proporcionaron respuestas correctas de la etapa de la metaconciencia.
Después de la enseñanza
El cuestionario presenta ocho preguntas abiertas, en secuencia de acuerdo a la propuesta institucional de la ENP, y en dos versiones “A” y “B”, se aplicó el cuestionario a un grupo de 25 estudiantes. Sólo cuatro de los 25 estudiantes (16%) proporcionaron respuestas correctas al cuestionario; las preguntas; 2, 3, 4, 5 y 8 (modalidad A) resultaron los más difíciles; ubicamos el desempeño de estos cuatro estudiantes en la etapa de la conciencia. Las respuestas incorrectas; de los 21 estudiantes restantes (84%), correspondieron al procesamiento no consciente.
El resultado es que hay muy poca comprensión de las ideas fundamentales de estadística y probabilidad resultante de la enseñanza en el aula, pero aun así en las aplicaciones de los dos cuestionarios casi todos los estudiantes intentaron resolver cada ejercicio. Las ideas más identificadas fueron: espacio muestra, medida de probabilidad y combinatoria, mientras que las ideas menos identificadas fueron: adición de probabilidad, regla del producto, variable aleatoria, espacio muestra. Los recursos semióticos más utilizados fueron: lengua natural, signos numéricos. Los otros conceptos matemáticos más identificados fueron: números reales positivos, operaciones aritméticas.
3. Tercera etapa: Análisis
Por sus respuestas a los cuestionarios exploratorios y por su disposición para ser entrevistados, se seleccionaron cuatro estudiantes; C1, C2, C3 y C4, y se les interrogó individualmente. Se aplicó la célula de análisis (Ojeda, 2006) a cada entrevista, las etapas de la subjetividad (Frawley, 1999) y el tipo de conocimiento (Pollastsek, 1981) adquirido por las respuestas de los casos interrogados.
El siguiente análisis, enmarcamos los reactivos referentes del interrogatorio en gris. En los pasajes citados, “E” denota al entrevistador, “C1 ” al caso entrevistado.
Reactivo “1B”:
En el año 1990 la población mundial de la Tierra era de 5292 millones de habitantes. Suponiendo que la tasa de crecimiento durante una década es de 18% y ésta se mantiene constante, ¿cuál será la población en los años 2000, 2010, 2020? Trazar su gráfica.
La Figura1 presenta la respuesta respectiva de C1 en el cuestionario.
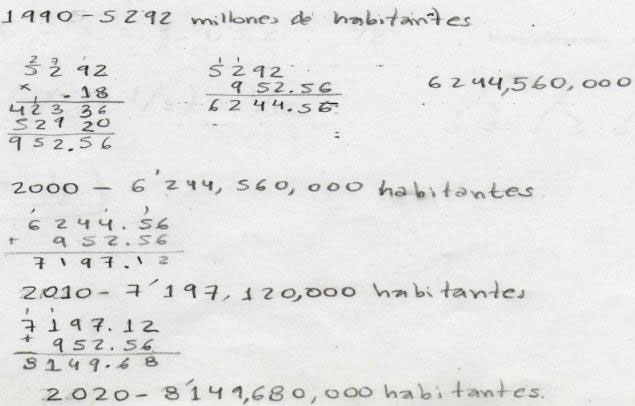
Figura 1. Respuestas del caso C1 al reactivo “1B”.
En general, C1 manifestó un razonamiento aditivo en lugar de multiplicativo, ya que el resultado del cálculo del porcentaje de crecimiento para la primera década es el mismo que se agregó a las décadas subsecuentes, en lugar de calcular sobre cada población el porcentaje indicado, ubicamos el conocimiento C1 de como funcional, aunque su respuesta es incorrecta.
2. [Lee el ejercicio y explica su respuesta rápidamente sin esperar a que se le realicen las preguntas], yo lo que hice fue como está expresado en porciento (%), multipliqué…. 5292 millones de habitantes por 0.18 para sacar lo que es el 18% de crecimiento en una década que es el equivalente a diez años; después, ese porcentaje lo sumé a los 5292 millones de habitantes para que me diera el total de habitantes que hace en una década [señala constantemente sus respuestas]… en el año 2000 y a esa misma cantidad le sumé el mismo porcentaje para que me diera la tasa de crecimiento en 20 años en el 2010 y volví a hacer lo mismo en la tercera etapa, que le sumé el 18% del porcentaje a la tercera etapa [a cada década le llama etapa], para que me diera el número de habitantes en 30 años. ¿Por qué lo manejé así? Porque para mí el 18%…y como dice que esto se mantiene constante fue un movimiento rectilíneo uniforme y no que va recto o lineal.
La lectura insuficiente del reactivo es clara en la intervención 8 de C1.
7.E. ¿Y tu gráfica?
8. Se me olvidó hacerla porque no leí.
En consecuencia, los recursos semióticos utilizados por fueron sólo arreglos numéricos, los signos numéricos en las operaciones aritméticas y, escasamente, la lengua natural escrita. Los términos utilizados durante la entrevista fueron habitantes, crecimiento, total, década y muestra (véase también la intervención 2 anterior).
Conclusiones
Esta investigación puso énfasis en el trabajo de los alumnos al tratar conceptos; de espacio muestra, evento, principio fundamental de conteo, análisis combinatorio y concepto de probabilidad. Organizados en equipo, el trabajo de los estudiantes dio oportunidad al profesor para promover sus reflexiones respecto a sus nociones de estadística y probabilidad.
Se observó que los alumnos no leen las instrucciones u observaciones que se les indican y ésta es también una limitante para no realizar bien los ejercicios..
Referencias
Frawley, W. (1999). Vygotsky y la ciencia cognitiva. Piadós, Barcelona.
Heitele, D. (1975). An Epistemological view on stochastics fundamental ideas. Educational Studies of Mathematics 6. Reidel, Holanda.
Infante, G. (1991). Métodos de enfoque interdisciplinario, Trillas, México.
Ojeda, A. M. (2006). Estrategia para un perfil nuevo de docencia: Un ensayo en la enseñanza de estocásticos. Matemática educativa, treinta años: una mirada fugaz, una mirada externa y comprensiva, una mirada actual. Santillana; Cinvestav del IPN. México, pp. 195-214.
ENP, (1996). Programa de estudios de la ENP 1996, clave 1712. Universidad Nacional Autónoma de México. Escuela Nacional Preparatoria. Aprobado por el H. Consejo Técnico 1996, México.
Pollatsek, S. Lima and A.D. Well. Concept or Computation: Students’ Understanding of the Mean. Educational Studies in Mathematics 12 (1981), pp. 191-204. D. Reidle Publishing Co.
Rivera, M. S. (2012). “COMPRENSIÓN DE IDEAS FUNDAMENTALES DE ESTOCÁSTICOS EN EL BACHILLERATO” . Editorial Académica Española. Alemania.
Gastos de envío
G R A T I S
G R A T I S
Envíos España península para pedidos superiores a 59,90 euros (más iva) (condiciones)
Imprimir
Tamaño original
Ampliar texto
Reducir texto
-
Se presenta un panorama general de la psicopatología infantil, desde los transtornos emocionales,a los problemas de alimentación o...16.40 € -
En este libro encontrarás 70 actividades para acompañar a los niños desde el respeto, el amor y la libertad enfocadas a respetar r...20.90 € -
La programación didáctica ELE es, como indica su subtítulo, "Pautas para el diseño de la programación de un curso ELE/L2"...6.76 € -
Mariana está a punto de descubrir la magia de los colores gracias a la ropa que escoje cada día al vestirse. El rosa la convierte...18.00 €
